日本語HOME 研究内容 経歴・業績 著作の補足・正誤表
（ギリシャ数学） 簡単な履歴と著作のリスト 正誤表はこちら

MENU

日本語HOME >著作の補足と正誤表> 数はどこから来たのか

last update 17/Aug/2013

『数はどこから来たのか：数学の対象の本性に関する仮説』のページ

ここではEnrico Giusti著，斎藤憲訳 『数はどこから来たのか：数学の対象の本性に関する仮説』（共立出版，1999年3月， 1999年5月2刷，四六版，178頁，2300円＋税）の訂正，追加などを行ないます．

本書は，数学の対象（数，群，曲線，集合などなど）が何であるのか，どのように生じたのかを問題にし，自然主義（これらの対象を自然界からの抽象であると する）や形式主義（公理によって定まる単なる記号と考える）の両方に反論し，効果的な問題解法の結晶化によって数学の対象が生じるという主張を打ち出して います．

記述は明快，平易で楽しめます．小冊子ですから，この一冊で数学史や数学論を全部学ぶわけにはいきませんが，これらの分野の見通しをよくしてくれる本です．数学史の通史を 読んだが全然面白くなかった，とか，大学で習ったガロア理論というのが結局何なのかどうも分からない，とかいう方に特にお薦めです．

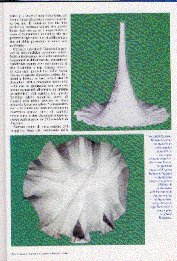ベルトラーミの「頭巾」 非ユークリッド幾何学のモデルとして有名なベルトラーミの「頭巾」です（本書p. 106参照）． Le Scienze (Scientific Americanのイタリア語版） aprile 2000, p.75より．

写真をクリックすると大きな写真が見られます

以下，例によって正誤表です．不手際をお詫びするとともに，ご指摘下さった方々に感謝いたします．

『数はどこから来たのか：数学の対象の本性に関する仮説』
正誤表Ver 2.00 (2000/05/19)
頁；行 誤 正
2; 5 Boronghjjieri Boringhieri 2刷で訂正済
15; 21 というという という
55; 16 立方の立方の立方 立立立方(cubocubocubis)
172; 13; reedition eは２つともアクサンティギュ 2刷で訂正済
172; 15 Dieudonne 最後のeにアクサンティギュ 2刷で訂正済
172; 注11 『原論』コンマンディーノによるイタリア語訳． 『原論』コンマンディーノによるイタリア語訳　[38]．
174; 7 oribgini origini 2刷で訂正済
追加情報

p.176 文献[83]には英訳があります．
L. Toti Rigatelli, Evariste Galois 1811-1832, Basel/Boston/Berlin: Birkhauser Verlag, 1996. (Birkhauserはaウムラウト)

（イタリア語原題の『バリケードの上の数学』のほうがいいのに．．．）

p.177 文献[88]は，ほぼ同じ内容の英語論文があります．

G. Vacca, "Maurolycus, the First Discovere of the Principle of Mathematical Induction," Bulletin of Amenrican Mathematical Society, 16(1909) 70--73.

なお，数学的帰納法の起源をめぐる論文として基本的なものは

  • H. Freudenthal, ``Zur Geschichte der vollstaendigen Induktion,'' Archives Internationales d'Histoires des Sciences XXII(1953), 17--37.

です．さらに最近の，ギリシアには数学的帰納法はなかったとするUnguruの論文， これに対するFolwerの反論，Unguruの再反論は一読の価値があります．
  • S. Unguru, ``Greek Mathematics and Mathematical Induction,'' Physis 28(1991) 273--289.
  • D. Fowler, ``Could the Greeks Have Used Mathematical Induction? Did They Use It?'' Physis 31(1994) 253--265.
  • S. Unguru, ``Fowling After Induction,'' Physis 31(1994) 267--272.

これに関連して，次の論文が印刷中とのことです．

  • Fabio Acerbi, ``Plato: Parmenides 149a7--c3: A Proof by Complete Induction?'' Archive for History of Exact Sciences, Forthcoming.

(2013年8月17日追記）もちろんこの論文は出版されています．Archive for History of Exact Sciences 55 (2000), 57--76. DOI: 10.1007/s004070000020です．その後ギリシャ数学史の研究で重要な論文を数多く発表して，現在なお活躍中のFabio Acerbiの最初の論文でした．なお，本書は2刷までいったのですが，その後の売れ行きが止まってしまって，まだ在庫があります．いい本なのですが．

著作の補足・正誤表に戻る

日本語HOME